学习笔记:扩散模型算法介绍

本文原写于2024年8月16日。
原理
扩散模型可实现从噪声(采样自简单分布,如高斯分布)到数据样本的转换,分为两个步骤:
- 固定的前向扩散过程\(q\):逐步向图片添加噪声直至得到一张纯噪声图像;
- 可训练的去噪过程\(p\):训练神经网络从纯噪声图像中去噪,得到一张真正的图片。
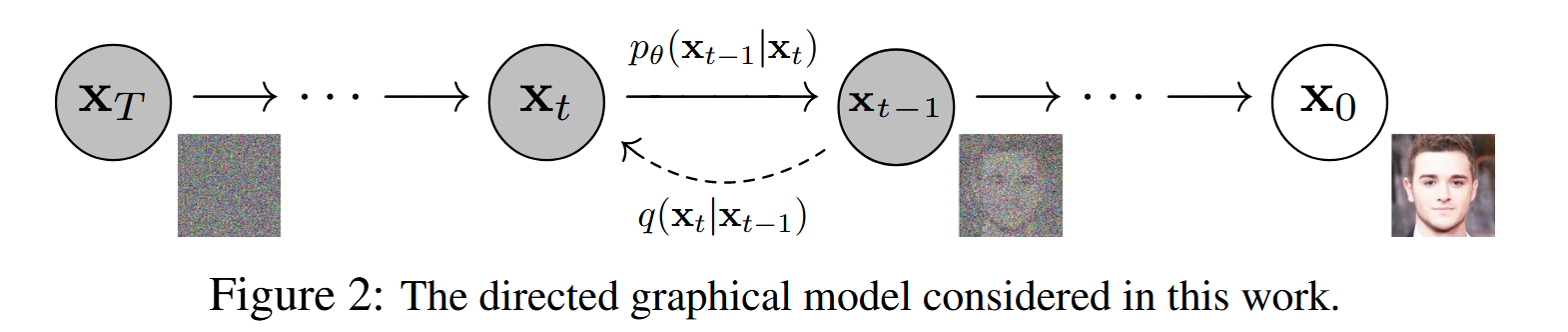
该过程是一个马尔可夫过程,因为计算\(\mathbf x_t\)只需要用到\(\mathbf x_{t-1}\),即当前时刻的状态仅由上一时刻的状态决定。
正向过程中,向原图像\(\mathbf x_0\)中不断混入高斯噪声,经过\(T\)次加噪,图像\(\mathbf x_T\)为符合标准高斯分布的纯噪声图像。网络的学习目标是学会\(T\)个去噪操作,将\(\mathbf x_T\)还原为\(\mathbf x_0\),每步去噪操作刚好抵消掉前面对应步骤的加噪操作。
前向与反向过程
前向过程
设来自某训练集的图像\(\mathbf x_0\)会被添加\(T\)次噪声,\(\mathbf x_T\)为最终生成的噪声图像,\(\mathbf x_t\)是这一时刻生成的图像,\(\mathbf x_{t-1}\)是上一时刻生成的图像。我们通常将正态分布设置为这个形式: \[ \mathbf{x}_t\sim\mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1},\beta_t\mathbf{I}) \]
\(\mathbf x_t\)可以通过一个服从标准正态分布的样本\(\epsilon_{t-1}\)算出: \[ \mathbf{x}_t=\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon_{t-1};\quad\epsilon_{t-1}\sim\mathcal{N}(0,\mathbf{I}) \]
\(\epsilon_t(t=1,2,\dots,T-1)\)是一组服从正态分布\(\mathcal{N}(0,\mathbf{I})\)的独立样本。
这里\(\beta_t\)不是常量,而是一个随时间\(t\)变化的变量,一般要越来越大,表示在给图像加噪的过程中,噪声的添加进度越来越快。将思维逆转过来,考虑反向去噪过程,一开始对纯噪声图像去噪较多,当图像越接近原图像时,去噪会越来越慢。
原论文中随着\(t\)的增大,\(\beta_t\)从1e-4到2e-2线性增长。
令\(\alpha_t=1-\beta_t\),\(\bar{\alpha_t}=\prod_{s=1}^t{\alpha_s}\),上式可化为 \[ \mathbf{x}_t=\sqrt{\alpha_t}\mathbf{x}_{t-1}+\sqrt{1-\alpha_t}\epsilon_{t} \]
接着向前递推,可做如下推导: \[ \begin{aligned} q\left( \mathbf{x}_t|\mathbf{x}_{t-1} \right) &=\sqrt{\alpha _t}\mathbf{x}_{t-1}+\sqrt{1-\alpha _t}\epsilon _{t}\\ &=\sqrt{\alpha _t}\left( \sqrt{\alpha _{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha _{t-1}}\epsilon _{t-1} \right) +\sqrt{1-\alpha _t}\epsilon _{t}\\ &=\sqrt{\alpha _t\alpha _{t-1}}\mathbf{x}_{t-2}+\sqrt{\alpha _t-\alpha _t\alpha _{t-1}}\epsilon _{t-1}+\sqrt{1-\alpha _t}\epsilon _{t}\\ &=\sqrt{\alpha _t\alpha _{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha _t\alpha _{t-1}}\epsilon \left( \text{正态分布相加还是正态分布} \right)\\ \vdots\\ &=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon\\ q\left( \mathbf{x}_t|\mathbf{x}_0 \right) &=\mathcal{N} \left( \mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,\left( 1-\bar{\alpha}_t \right) \mathbf{I} \right)\\ \end{aligned} \]
如此我们就可以直接从\(\mathbf{x}_0\)推导出\(\mathbf{x}_t\)。
反向过程
该过程我们希望能倒过来取消每一步的加噪操作,使一幅纯噪声图像\(\mathbf{x}_T\)变回数据集中的图像\(\mathbf{x}_0\),利用这个过程,我们可以把任意一个从标准正态分布采样的噪声图像变成一幅和训练数据相近的图像,从而达到图像生成的目的。
数学上有:当\(\beta_t\)足够小时,每一步的加噪逆操作仍然满足正态分布 \[ \mathbf{x}_{t-1}\sim\mathcal{N}(\tilde{\mu}_t,\tilde{\beta}_t\mathbf{I}) \]
为了描述去噪操作,神经网络的任务就是根据当前时刻\(t\)、当前图像\(\mathbf{x}_t\)拟合当前加噪逆操作的正态分布,即拟合当前的均值\(\tilde{\mu}_t\)和方差\(\tilde{\beta}_t\)。事实上,由于加噪的操作是固定的,因此理论上去噪的操作(即加噪的逆操作)也是固定的,但该操作极难从理论上求得,只能用神经网络去尽量拟合。
虽然我们无法得到逆转过程的概率分布\(q\left( \mathbf{x}_{t-1}|\mathbf{x}_t \right)\),但如果知道\(\mathbf x_0\),则可以直接由贝叶斯公式计算出\(q\left( \mathbf{x}_{t-1}|\mathbf{x}_t ,\mathbf x_0\right)\): \[ q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)=q(\mathbf{x}_t|\mathbf{x}_{t-1},\mathbf{x}_0)\frac{q(\mathbf{x}_{t-1}|\mathbf{x}_0)}{q(\mathbf{x}_t|\mathbf{x}_0)} \]
等式左边(其中均值和方差是待求项): \[ q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t-1};\tilde{\mu}_t,\tilde{\beta}_t\mathbf{I}) \]
等式右边: \[ \begin{aligned} q(\mathbf{x}_t|\mathbf{x}_{t-1},\mathbf{x}_0)&=\mathcal{N} (\mathbf{x}_t;\sqrt{1-\beta _t}\mathbf{x}_{t-1},\beta _t\mathbf{I})\\ q(\mathbf{x}_t|\mathbf{x}_0)&=\mathcal{N} (\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,(1-\bar{\alpha}_t)\mathbf{I})\\ q(\mathbf{x}_{t-1}|\mathbf{x}_0)&=\mathcal{N} (\mathbf{x}_{t-1};\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0,(1-\bar{\alpha}_{t-1})\mathbf{I})\\ \end{aligned} \]
等式右边全部已知,代入可得给定\(\mathbf x_0\)时的去噪分布。
经过化简可得分布均值与方差: \[ \begin{aligned} \tilde{\mu}_t&=\frac1{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_{t}\right)\\ \tilde{\beta}_t&=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot\beta_t \end{aligned} \] 其中\(\epsilon_{t}\)来自式(3)。观察上式可知,方差\(\tilde{\beta}_t\)是一个常量,与输入\(\mathbf x_0\)无关,训练去噪网络时仅需要拟合均值即可。再次观察目标均值公式,式中唯一不确定的值只有\(\epsilon_{t}\)。因此,直接让神经网络预测一个噪声\(\epsilon_\theta(\mathbf x_t,t)\)让它和生成\(\mathbf x_t\)的噪声\(\epsilon_t\)的均方误差最小即可。对于一轮训练,误差函数可写成 \[ L=||\epsilon_t-\epsilon_\theta(\mathbf{x}_t,t)||^2 \]
训练算法与采样算法
训练算法

逐行分析算法含义: 2. 从训练集中取出一个数据\(\mathbf x_0\) 3. 随机从\(1,2,\dots,T\)中取出一个时刻训练(虽然要求神经网络拟合\(T\)个正态分布,但实际训练时,不用一轮预测\(T\)个结果,只需要随机预测\(T\)个时刻中某一个时刻的结果就行) 4. 随机生成一个噪声\(\epsilon\) 5. 将\(\mathbf x_t,t\)传给神经网络,通过梯度下降预测随机噪声\(\epsilon_\theta(\mathbf{x}_t,t)\) 6. 训练到收敛位置(时间较长,通常设\(T=1000\))
采样(测试)算法

- 从标准高斯分布采样一个噪声图像
- 循环迭代
- 如果时间步不为1,从高斯分布采样一个噪声\(z\),否则\(z=0\)
- 计算每个时间步\(t\)的噪声图(\(\epsilon_\theta(\mathbf x_t,t)\)由训练步骤获得)
以上是关于扩散模型的粗略解读。部分推导未在本文列出,除非研究目标是改进扩散模型本身,学习时了解该模型整体思想和主要原理即可。
- Title: 学习笔记:扩散模型算法介绍
- Author: Jachin Zhang
- Created at : 2025-02-06 20:04:45
- Updated at : 2025-03-04 21:18:48
- Link: https://jachinzhang1.github.io/2025/02/06/DiffusionModel/
- License: This work is licensed under CC BY-NC-SA 4.0.